Jugando Con Las Matemáticas
Si quieres tu puedes
INSTITUCIÓN EDUCATIVA ERNESTO PARODI MEDINA
ÁREA: MATEMÁTICAS TEMA: VECTORES
DOCENTE: JOEL FERNÁNDEZ VARGAS
Suma de vectores por descomposición de vectores
Hasta ahora solo se han sumado dos vectores, de tal manera que para sumar más de dos es conveniente utilizar el método de descomposición vectorial, para lo cual es necesario conocer y encontrar las componentes rectangulares de un vector
Componentes rectangulares de un vector: Dado un vector cualquiera que no sea paralelo al eje de las X o aleje de las Y, siempre es posible expresarlo como la suma de dos vectores que uno de los cuales sea paralelo al eje X y el otro paralelo al eje de la Y. para los cual es necesario utilizar las relaciones trigonométricas
Ej10
. Encontrar las componentes rectangulares del vector m cuya magnitud es de 500 u y su dirección θ = 35°
Sol:
Para resolver el ejerció es conveniente ubicar el vector en el plano cartesiano de acuerdo a sus características
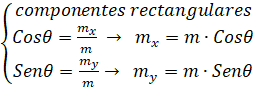

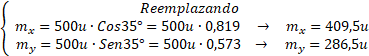
Al sumar vectores por descomposición vectorial lo que en realidad se hace es descomponer todos los vectores en sus componentes rectangulares de tal manera que reduzcamos los vectores iniciales a una suma (algebraica) de:
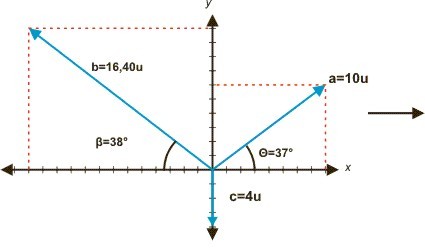
Hallar el vector resultante de los vectores a, b y c cuyas magnitudes son 10u, 16,40u y 4u unidades respectivamente, ver gráfica
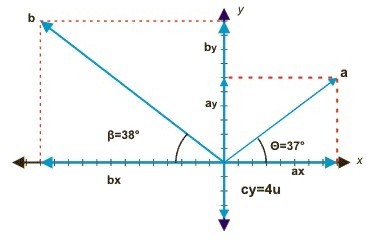
Componentes |
Ecuación |
Reemplazo |
Valor |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
No hay componente en |
||
|
|
|
|
Encontremos |
|
|
|
|
|
|
|
Reemplazando estos valores en la ecuación
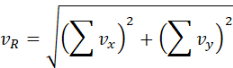
![]()
![]()
![]()
![]()
Para encontrar la dirección del vector resultante utilizamos
![]()
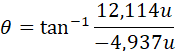
![]()
![]()
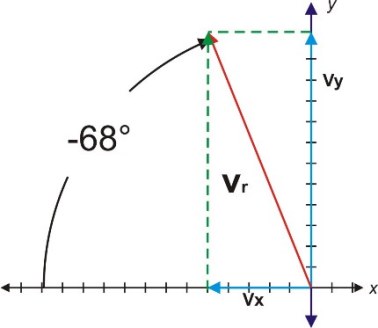
Diferencia de vectores
Para restar dos vectores a y b o hallar su diferencia a - b (que entre otras cosas es diferente de b - a ), solo hay que realizar una suma de el vector a con el inverso aditivo de b, es decir:
![]()
Hallar el vector p - q, sabiendo que p = 6u con una dirección de θ = -40° y q =4u con una dirección de β = 60°
Con los datos que hay en la gráfica, con las magnitudes de los vectores dadas se puede utilizar el teorema del seno y el coseno para encontrar el vector resultante p - q
SUGERENCIA: Para resolver el ejercicio es necesario encontrar el ángulo α y λ pero θ = λ por ser alternos y β = α por ser opuestos por el vértice



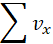 y
y